解题四步法(黄金法则)
如何变化,解决函数应用题都可以遵循以下四个核心步骤,形成固定的解题思维模式。
第一步:审题建模——将文字语言转化为数学语言
这是最关键的一步,目标是读懂题意,提炼变量,建立函数模型。

- 抓关键词:仔细阅读题目,圈出与数量、变化、目标相关的关键词,如“成本”、“利润”、“收益”、“速度”、“时间”、“最大”、“最小”、“总量”、“单价”、“固定值”、“变量”等。
- 设未知数:根据问题,选择一个或多个自变量,通常选择题目中描述其变化的量为自变量
x,然后根据题意,用x来表示其他相关量。 - 建函数关系:利用题目中给出的等量关系(如利润 = 收入 - 成本,路程 = 速度 × 时间等),将因变量
y用自变量x的解析式表示出来,得到y = f(x)。 - 定定义域:这是最容易忽略但又至关重要的一步! 根据实际问题的意义(如数量不能为负、人数必须为整数等),确定自变量
x的取值范围,即函数的定义域。
【示例】
某商品每件成本 40 元,售价 60 元,每月可售出 100 件,市场调查显示,若每件售价提高 1 元,销量就减少 1 件,若要使每月利润最大,售价应定为多少?
-
审题建模:
- 成本、售价、销量、利润、最大。
- 设未知数:设售价提高
x元,则当前售价为60 + x元。 - 建函数关系:
- 销量 =
100 - x件 - 每件利润 =
(60 + x) - 40 = 20 + x元 - 总利润
y= 每件利润 × 销量 =(20 + x)(100 - x)
- 销量 =
- 定定义域:
- 售价提高
x元,x可以为 0 或正数。 - 销量
100 - x必须 ≥ 0,x ≤ 100。 - 综上,定义域为
[0, 100]。
- 售价提高
得到模型:求函数
y = (20 + x)(100 - x)在区间[0, 100]上的最大值。 (图片来源网络,侵删)
(图片来源网络,侵删)
第二步:解模——利用数学工具求解函数模型
这一步是纯粹的数学计算,目标是求出函数的极值或特定值。
- 明确目标:题目要求什么?是求最大值、最小值、零点,还是求某个特定点的函数值?
- 选择方法:
- 二次函数:对于
y = ax² + bx + c(a ≠ 0),可通过配方法或顶点公式x = -b/(2a)求最值。 - 基本初等函数:如指数函数、对数函数,利用其单调性求解。
- 导数法(高中重点):对于更复杂的函数,通过求导,找到导数为零的点(驻点),然后判断其极值性质。
- 均值不等式:对于特定形式的函数(如两正数之和为定值,求积的最大值),可考虑使用。
- 二次函数:对于
【示例续】
模型为
y = (20 + x)(100 - x) = -x² + 80x + 2000,定义域[0, 100]。
- 解模:
- 这是一个开口向下的二次函数,其最大值在顶点处取得。
- 使用顶点公式,
x = -b/(2a) = -80 / (2 × -1) = 40。 x = 40在定义域[0, 100]内。- 当售价提高 40 元时,利润最大。
第三步:作答——将数学答案还原为实际问题
这一步是“翻译”过程,目标是用清晰、完整的语言回答题目提出的问题。
- 回归问题:你的计算结果是
x = 40,但题目问的是“售价应定为多少?” - 计算最终答案:售价 = 原价 + 提高价 =
60 + 40 = 100元。 - 完整作答:答:若要使每月利润最大,售价应定为 100 元。
第四步:反思检查——确保答案的合理性与完整性
- 检查单位:答案的单位是否正确?(如元、件、米等)
- 检查合理性:答案是否符合常理?(如人数不能是小数,售价不能为负数)
- 检查计算:重新快速核对一遍计算过程,避免低级错误。
核心能力培养
除了四步法,以下几种能力是解决复杂函数应用题的基石。
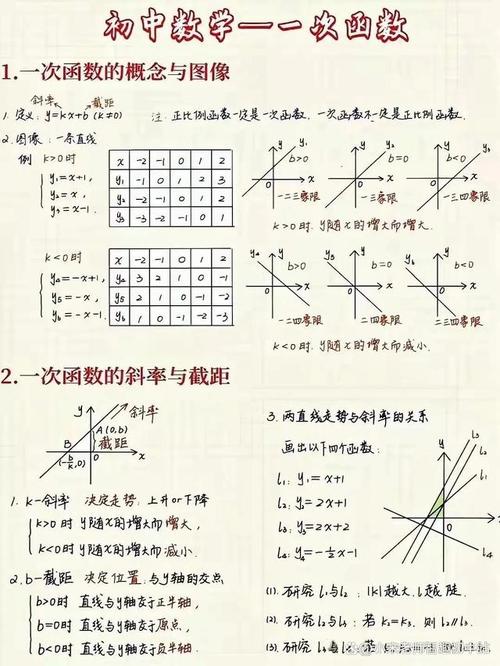
识别函数类型的能力
要能快速判断它可能属于哪种函数模型。
- 一次函数 (
y=kx+b):匀速变化问题,如匀速直线运动、成本问题(固定成本+可变成本)。 - 二次函数 (
y=ax²+bx+c):最优化问题,如利润最大、成本最低、面积最大、最远/最近问题等。 - 指数函数 (
y=a·b^x+c):增长率/衰减率问题,如人口增长、银行复利、细胞分裂、放射性衰变等,关键词是“按...%增长/衰减”。 - 分段函数:问题在不同阶段遵循不同的规律,如出租车计费、个人所得税、水电阶梯计价等,关键词是“超过...部分按...计算”。
提炼信息与转化信息的能力
这是“建模”的核心,练习将长段文字描述拆解成数学条件。
- “A比B多x” →
A = B + x - “A是B的k倍” →
A = kB - “A与B成反比” →
A = k/B - “售价每增加1元,销量减少2件” →
销量 = 初始销量 - 2 × (售价 - 初始售价)
数形结合的能力
- 画示意图:对于几何问题(如面积、体积),动手画出图形,标出变量,能帮助你更直观地发现等量关系。
- 画函数草图:在求解最值时,画出函数的大致图像(特别是定义域内的部分),可以帮助你判断极值出现在端点还是内部,避免遗漏。
分类讨论的思想
中的变量有多种可能情况或函数在定义域内性质不唯一时,必须进行分类讨论。
- 典型场景:
- 求解含绝对值的函数问题。
- 函数的参数不确定,需要讨论参数的不同取值对函数性质的影响。
- 函数在定义域内不单调,可能有多个极值点,需要比较它们的大小。
避坑指南(常见错误)
- 忽略定义域:这是最常见的错误!函数的图像可能无限延伸,但实际问题不行,一定要根据题意给
x加上“紧箍咒”。 - 设错变量:自变量
x的选择要服务于求解目标,有时直接设所求量为x会更简单,有时设中间变量x更方便建立关系,需要灵活选择。 - 混淆变量关系:在建立函数关系时,要搞清楚谁是自变量,谁是因变量,谁依赖于谁,避免把关系弄反。
- 答非所问:解出
x后,一定要看清题目问的是什么,是x本身,还是x的某个函数值,或是其他相关量。 - 计算粗心:展开括号、移项、配方、求导等步骤要细心,尤其是在考试中,一个符号的错误会导致全盘皆输。
解决函数应用题,就像当一名侦探和翻译家:
- 侦探:从复杂的案情(题目)中找到线索(数量关系)。
- 翻译家:将案情语言翻译成数学语言(函数模型)。
- 数学家:用数学工具(解模)破解谜题。
- 通讯员:将数学答案翻译回案情语言(作答)。
多练、多思、多总结是掌握这些技巧的唯一途径,每做完一道题,都回顾一下自己是如何完成这四步的,特别是“建模”和“定定义域”的过程,你的解题能力一定会稳步提升!