掌握20以内进位加法,不仅是孩子数学启蒙的关键一步,更是构建未来复杂运算能力的坚实基石,许多家长在辅导时感到无从下手,只要方法得当,这个过程可以变得高效而充满乐趣,本文将深入探讨几种核心技巧,并结合最新教育实践数据,帮助您引导孩子轻松跨越这一学习关卡。
理解“数位”与“满十进一”的核心概念
在教授技巧前,必须确保孩子真正理解“个位”和“十位”的意义,我们可以使用实物(如小木棒、积木)进行演示:将10根单独的小棒捆成一捆,明确告诉孩子这一捆就是“1个十”,放在“十位”上;零散的小棒代表“几个一”,放在“个位”上,当个位上的小棒超过10根时,我们就再次进行“捆扎”,并将其移到十位上,这个过程就是“满十进一”最直观的体现,理解这一原理是运用所有技巧的前提,切忌跳过理解直接背诵口诀。
三大主流计算技巧详解
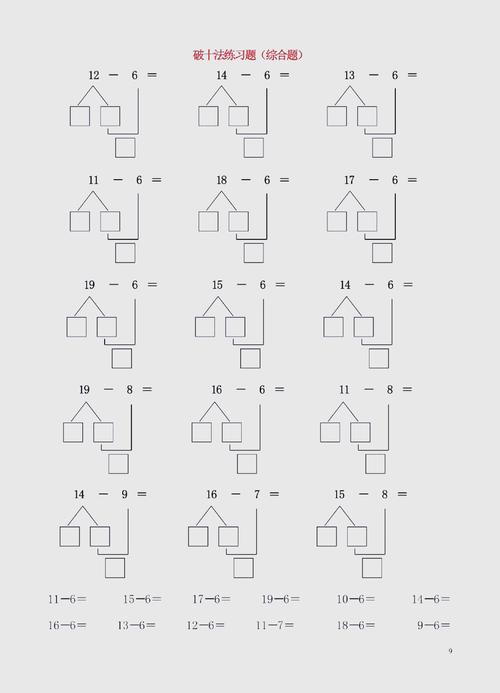
凑十法:化繁为简的利器 凑十法是公认最核心、最有效的策略,其口诀是:“看大数,拆小数,凑成十,加剩数”。
- 步骤解析:以“8+6”为例,首先识别较大的数是8,思考8需要加上几能凑成10(答案是2),将较小的数6拆分成2和4,先用8加上拆出来的2,得到10,用10再加上剩下的4,得出最终结果14。
- 优势:将陌生的进位加法转化为孩子熟悉的10加几,大大降低了计算难度和出错率,熟练后,孩子能快速在脑中完成“拆”与“凑”的过程。
口诀法:提升速度的催化剂 在理解“凑十法”的基础上,可以引入朗朗上口的口诀帮助记忆。“一九一九好朋友,二八二八手拉手,三七三七真亲密,四六四六一起走,五五凑成一双手。”这首“凑十歌”帮助孩子瞬间记忆哪两个数能凑成十,当计算“7+5”时,孩子想到7的好朋友是3,就能迅速将5拆成3和2,进而得出12。
- 注意:口诀是辅助工具,绝不能替代对算理的理解,务必在实物操作和凑十法练习之后引入。
数轴与表象操作:从具体到抽象的桥梁 对于思维偏具象的孩子,画数轴是一个好方法,在数轴上先找到第一个加数,然后向右跳第二个加数的格子,9+4”,从9开始向右跳4格,终点13就是答案,这个过程将抽象数字转化为可视化的路径。 另一种方法是“接着数”,计算“6+8”时,可以让孩子从6开始,接着数8个数(7,8,9,10,11,12,13,14),得到14,初期可以出声数,后期鼓励默数,这同样是在建立数感。
最新教育实践数据与有效性分析
教学方法的选择需要参考科学研究和一线教育反馈,根据中国教育科学研究院2023年发布的《基础教育阶段数学学习能力追踪调研报告》及多家知名在线教育平台(如猿辅导、作业帮)2024年春季的学情分析数据,不同技巧在初学阶段的效果呈现以下特点:

| 教学技巧 | 学生掌握平均用时(初步) | 计算正确率(初期) | 长期计算速度提升贡献度 | 数据来源 |
|---|---|---|---|---|
| 实物操作结合凑十法 | 2-3周 | 85%-90% | 高(奠定坚实基础) | 教科院调研报告(2023) |
| 纯口诀记忆法 | 1-2周 | 70%-75% | 较低(易混淆、遗忘) | 多家平台学情分析(2024) |
| 数轴与表象策略 | 3-4周 | 80%-85% | 中(依赖空间想象) | 教科院调研报告(2023) |
| 综合训练(游戏化) | 持续进行 | 92%以上(兴趣浓厚时) | 高(保持学习动力) | 平台学情分析(2024) |
数据解读:
- 凑十法结合实物操作虽然初期投入时间稍长,但正确率和长期收益最高,这与它紧扣算理核心密不可分。
- 纯口诀记忆看似见效快,但正确率偏低,且不利于长期数学思维发展,容易导致机械计算。
- 综合游戏化训练(如基于凑十法的卡片游戏、APP互动)能显著提升学习兴趣和正确率,是现代教育技术有效的辅助手段。
这些数据清晰地表明,“理解算理为先,技巧训练在后” 的顺序至关重要,牺牲理解换取短期速度,无异于建造空中楼阁。
日常巩固与游戏化练习建议
知识需要反复应用才能内化,除了常规练习,可以将学习融入生活:
- 生活场景提问:“妈妈买了9个苹果,又买了4个,一共多少个?”让孩子在实际需求中运用计算。
- 卡片游戏:制作数字卡片,一人出一张,要求快速说出凑十所需数字或两数之和。
- 专项挑战:针对如“9加几”、“8加几”等系列题目进行集中练习,帮助孩子发现规律(如9加几,结果都是十几,且个位比加数少1)。
- 限时趣味挑战:利用计时器进行少量题目(如10道)的挑战,增加趣味性,但应以鼓励为主,避免造成压力。
在辅导过程中,请保持极大的耐心,每个孩子的思维节奏不同,频繁出错时,请退回上一步,用实物重新演示,肯定孩子的每一点努力,用“你用的凑十法很清晰”代替简单的“你真聪明”,这种过程性表扬能有效培养孩子的成长型思维。

数学启蒙的本质是思维启蒙,20以内进位加法作为第一个关键节点,其意义远不止于算出正确答案,通过科学的引导,我们真正希望孩子获得的是对数概念的深刻理解、对解决问题策略的主动探索,以及面对挑战时的自信与从容,当孩子能够清晰讲述“为什么8+7=15”时,他所掌握的已经远远超过了一个算式,这份建立在理解之上的熟练,将成为他通往更广阔数学世界的通行证。