基本原则

在掌握具体技巧前,必须先打好基础，养成好习惯。

1. “一看、二想、三算、四查”

   
   （图片来源网络，侵删）
   • 一看：看清题目中的数字、运算符号和运算顺序，这是最关键的一步，很多错误源于看错数字或符号。
   • 二想：思考用什么方法计算最简便，不要提笔就算。
   • 三算：按照想好的方法认真计算，书写工整，数位对齐。
   • 四查：计算完成后，立即进行检查，可以重新算一遍，或者用逆运算、估算等方法验证。

2. 强化“数感”

   • 数感是对数字的直观感知,比如看到 98，能立刻想到 100-2；看到 25，能想到 100÷4，培养数感是灵活运用所有技巧的前提。

3. 熟记“基本口诀”

   • 20以内加减法：必须达到脱口而出的程度。
   • 乘法口诀：不仅要会顺着背，还要会倒着背、随机抽问，做到“任意两个一位数相乘，瞬间出答案”。
   • 常用数据：牢记 25×4=100, 125×8=1000, 15×4=60 等特殊组合。

核心通用技巧

这些技巧适用于大部分口算题,是提高速度的“利器”。

凑整法

这是口算最核心、最常用的技巧，核心思想是“凑成整十、整百、整千的数”。

• 加法凑整：

  • 拆数凑整：看到接近整十、整百的数，先拆开。
  • 例：37 + 58 = ?
    • 思路：把 37 拆成 30 + 7，把 58 拆成 50 + 8。
    • 计算：30 + 50 = 80，7 + 8 = 15。
    • 结果：80 + 15 = 95。
  • 交换凑整：利用加法交换律和结合律。
  • 例：78 + 46 + 22 = ?
    • 思路：46 和 22 凑整是 68。
    • 计算：78 + (46 + 22) = 78 + 68。
    • 再凑整：78 + 68 = (70 + 8) + (60 + 8) = 130 + 16 = 146。

• 减法凑整：

  • 拆数凑整：
  • 例：81 - 39 = ?
    • 思路：把 39 看成 40 - 1。
    • 计算：81 - 40 + 1 = 41 + 1 = 42。
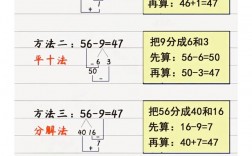
  • 例：156 - 98 = ?
    • 思路：把 98 看成 100 - 2。
    • 计算：156 - 100 + 2 = 56 + 2 = 58。

• 乘法凑整：

  • 例：25 × 16 = ?
    • 思路：利用 25 × 4 = 100。
    • 计算：25 × 16 = 25 × (4 × 4) = (25 × 4) × 4 = 100 × 4 = 400。
  • 例：125 × 24 = ?
    • 思路：利用 125 × 8 = 1000。
    • 计算：125 × 24 = 125 × (8 × 3) = (125 × 8) × 3 = 1000 × 3 = 3000。

运算定律的灵活运用

• 加法交换律/结合律：a + b = b + a，(a + b) + c = a + (b + c)，主要用于凑整。
• 乘法交换律/结合律：a × b = b × a，(a × b) × c = a × (b × c)，主要用于凑整和简化计算。
• 乘法分配律：(a + b) × c = a × c + b × c，这是口算的“大杀器”。
  • 例：102 × 5 = ?
    • 思路：把 102 拆成 100 + 2。
    • 计算：(100 + 2) × 5 = 100 × 5 + 2 × 5 = 500 + 10 = 510。
  • 例：45 × 11 = ?
    • 思路：把 11 拆成 10 + 1。
    • 计算：45 × (10 + 1) = 45 × 10 + 45 × 1 = 450 + 45 = 495。

特殊数字的记忆法

• 5的倍数：个位是0或5。
• 2的倍数（偶数）：个位是0, 2, 4, 6, 8。
• 4的倍数：一个数的末两位数是4的倍数。
• 25的倍数：一个数的末两位数是 00, 25, 50, 75。
• 特殊组合：
  • 5 × 2 = 10
  • 25 × 4 = 100
  • 125 × 8 = 1000
  • 11 × 几：两边一拉，中间相加（如 11 × 23 = 253，注意进位，如 11 × 59 = 649）。

分题型专项技巧

加法

• 进位加法：从高位算起，记住进位数，如 47 + 35，先算 40 + 30 = 70，再算 7 + 5 = 12，70 + 12 = 82。
• 多位数加法：分步计算，心算出结果，如 325 + 478，可以心算 300 + 400 = 700，25 + 78 = 103，700 + 103 = 803。

减法

• 退位减法：从高位算起，记住借位数，如 81 - 37，先算 80 - 30 = 50，再算 11 - 7 = 4，50 + 4 = 54。
• 多位数减法：分步计算，如 512 - 345，可以心算 500 - 300 = 200，12 - 45 不够减，所以从 200 里借 100，变成 112 - 45 = 67，100 + 67 = 167。

乘法

• 两位数乘一位数：拆分法，如 24 × 3，20 × 3 = 60，4 × 3 = 12，60 + 12 = 72。
• 两位数乘整十数：先乘以“0”前面的数，再在末尾加“0”，如 14 × 30，先算 14 × 3 = 42，再在末尾加一个“0”，得 420。
• 两位数乘两位数：
  • 竖式心算法：在脑子里列竖式，如 23 × 14，先算 23 × 4 = 92，再算 23 × 10 = 230，92 + 230 = 322。
  • 凑整法：如 19 × 8，把 19 看成 20 - 1，20 × 8 - 1 × 8 = 160 - 8 = 152。

除法

• 除数是一位数：利用乘法口诀反推，如 72 ÷ 9，想 9 和几相乘得 72，是 8。
• 整十数除法：先不看末尾的“0”，算完后再把“0”加上或去掉，如 120 ÷ 6，想 12 ÷ 6 = 2，再在末尾加一个“0”，得 20。
• 估算：当不能整除时，用估算，如 89 ÷ 9，想 9 和 9 相乘最接近 89，9 × 9 = 81，89 - 81 = 8，所以商是 9，余数是 8。

训练建议

1. 每日坚持：每天进行5-10分钟的口算练习，贵在坚持。
2. 由易到难：从一位数运算开始，逐步过渡到两位数、三位数，再到混合运算。
3. 计时训练：规定时间完成一定数量的题目，可以激发孩子的紧迫感和成就感。
4. 趣味化：使用口算卡片、口算APP、游戏等方式，让练习不那么枯燥。
5. 错题本：准备一个错题本，记录做错的题目和原因，定期复习，避免重复犯错。
6. 鼓励与表扬：多鼓励孩子，表扬他的进步，建立自信心。

总结一下：小学口算的核心是“凑整”和“运用定律”，家长在辅导时，不要只满足于孩子算对了，更要引导他思考“有没有更简单的方法？”，当孩子能主动寻找最优解法时，他的数学思维就真正开始发展了，希望这些技巧能帮助您的孩子爱上口算，学好数学！