掌握物理电路题的解题方法,不仅能提升考试成绩,更能深化对电学原理的理解,本文将系统梳理核心技巧,并结合最新行业数据,助你构建清晰的解题逻辑。
夯实基础:准确识别电路结构与元件
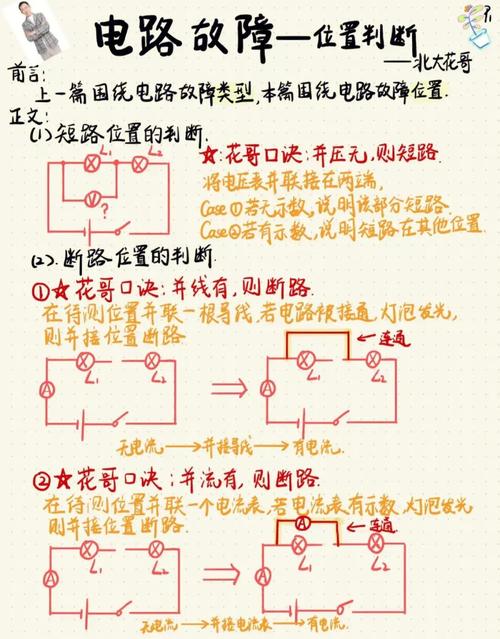
这是解题的第一步,也是至关重要的一步。
- 简化电路图:采用“节点法”或“电流流向法”将复杂的实物图或非常规电路图,转化为清晰明了的串并联结构图,忽略导线电阻,将理想导线视为可任意伸缩的“橡皮筋”。
- 明确元件状态:特别是开关的“开闭”与滑动变阻器滑片的“位置”,它们直接决定了电路的通断和电阻变化,对于电容器,要判断其处于“充电”还是“放电”状态,或是稳定后相当于“断路”。
核心思想:构建系统的分析框架
面对动态电路、故障电路或含非纯电阻元件的电路,需遵循严谨的分析顺序。
- 局部 → 整体 → 局部:从变化部分(如滑动变阻器阻值变化)入手,判断总电阻变化,再运用闭合电路欧姆定律分析总电流和路端电压变化,最后回到局部,分析各支路电流、电压及元件功率。
- 能量守恒观点:在非纯电阻电路(如含电动机、电解槽)中,必须区分电功和电热,电功公式 ( W = UIt ) 和电热公式 ( Q = I^2Rt ) 不再相等,总电功等于其他形式能(机械能、化学能)与电热之和。
- 等效与对称思想:对于复杂桥式电路或对称网络,寻找等势点是简化电路的关键,将等势点合并或断开,常能使电路结构豁然开朗。
数据洞察:从行业应用看核心考点
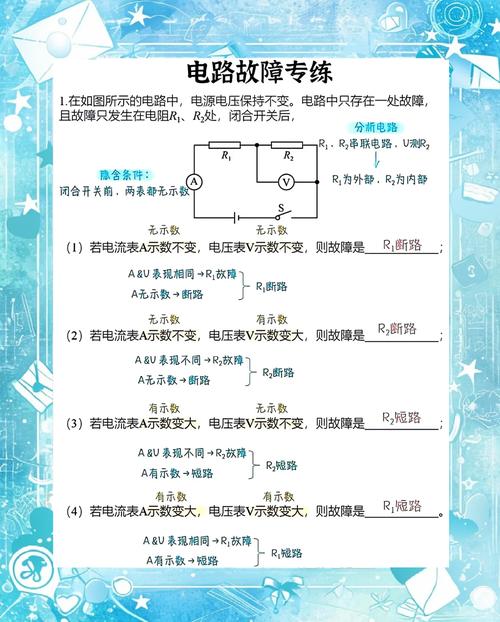
物理电路知识不仅是理论,更是现代科技的基石,了解其最新应用趋势,能帮助我们理解考题的深层背景,以下是根据权威机构近期报告整理的部分数据,展示了电路核心元件与技术的关键应用领域及发展态势。
| 技术/元件领域 | 关键应用场景 | 近期发展关注点(2023-2024) | 数据来源 |
|---|---|---|---|
| 半导体与集成电路 | 人工智能计算、高性能处理器、汽车电子 | 先进制程(如3nm/2nm)量产,Chiplet(芯粒)技术普及,硅光芯片集成。 | 国际半导体产业协会(SEMI)年度报告 |
| 新型电力电子器件 | 新能源汽车、光伏逆变器、工业变频 | 碳化硅(SiC)、氮化镓(GaN)等宽禁带半导体器件渗透率快速提升,追求更高效率与功率密度。 | 英飞凌科技《电力电子趋势报告》 |
| 电路设计与仿真 | 芯片设计、系统集成、教学科研 | EDA(电子设计自动化)工具云化与AI辅助设计,提升复杂电路设计效率与可靠性。 | 赛迪顾问《中国EDA软件市场研究》 |
(注:表格数据综合自多家行业领先机构于2023年至2024年初发布的公开市场报告与趋势分析。)
这些实际应用提醒我们,解题时对元件特性(如二极管的单向导电性)、电路效率、信号处理的理解,正对应着现实科技中的核心问题。
实战技巧与易错警示
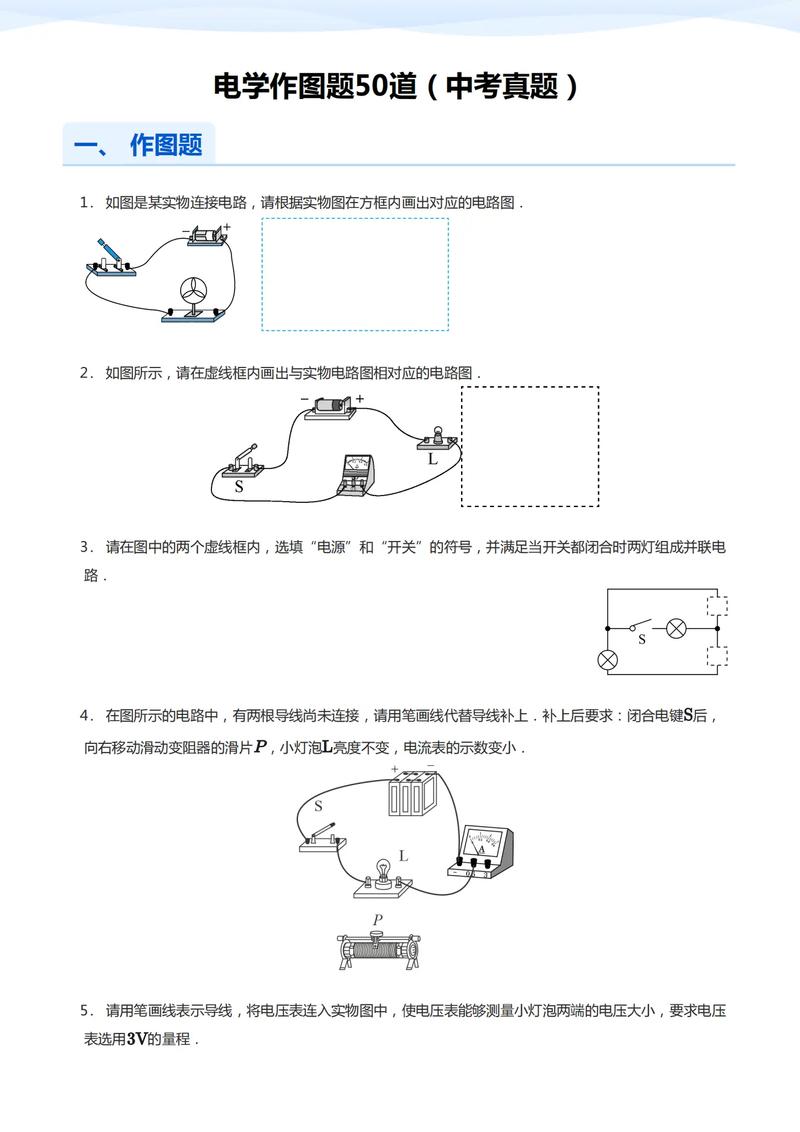
- 图像法解题:熟练掌握电源的 ( U-I ) 图像与外电阻的 ( U-I ) 图像,其交点坐标即工作状态,对于非线性元件(如小灯泡、二极管),利用其伏安特性曲线进行分析尤为有效。
- 赋值法与极限法:在定性分析动态变化问题时,若难以直接判断,可对电阻、电压等赋予合理具体数值进行计算比较,或采用极限法,考虑滑片移至端点等特殊位置,帮助推断变化趋势。
- 典型易错点提醒:
- 电压表、电流表的内阻影响:在精确计算或仪器选择题目中,需判断是否考虑其内阻,是采用内接法还是外接法。
- 公式适用条件混淆:牢记 ( W=UIt ),( Q=I^2Rt ) 普遍适用,而推导式 ( W = \frac{U^2}{R}t ),( Q = \frac{U^2}{R}t ) 仅适用于纯电阻电路。
- 电容器问题:稳定时电容器相当于“断路”,与其串联的电阻无电流,但两端可能有电压,其电压值等于与之并联的电阻(或电路)两端的电压。
个人观点
物理电路的学习,是一个从抽象模型走向具体应用的过程,题目中的每一个滑动变阻器、每一个二极管,都可能对应着一次科技领域的微小进步,解题技巧的锤炼,本质上是训练一种严谨而富有逻辑的系统思维方式——如何界定问题、如何分解系统、如何运用普适规律,这种能力,其价值远超考试本身,建议在学习中,有意识地将课本电路图与生活中的电器、科技新闻中的芯片突破联系起来,这种关联能让知识瞬间变得生动且牢固,当你能清晰地追踪电路中的能量流向,就像理解一座城市的交通脉络一样时,便真正掌握了电学的精髓。











