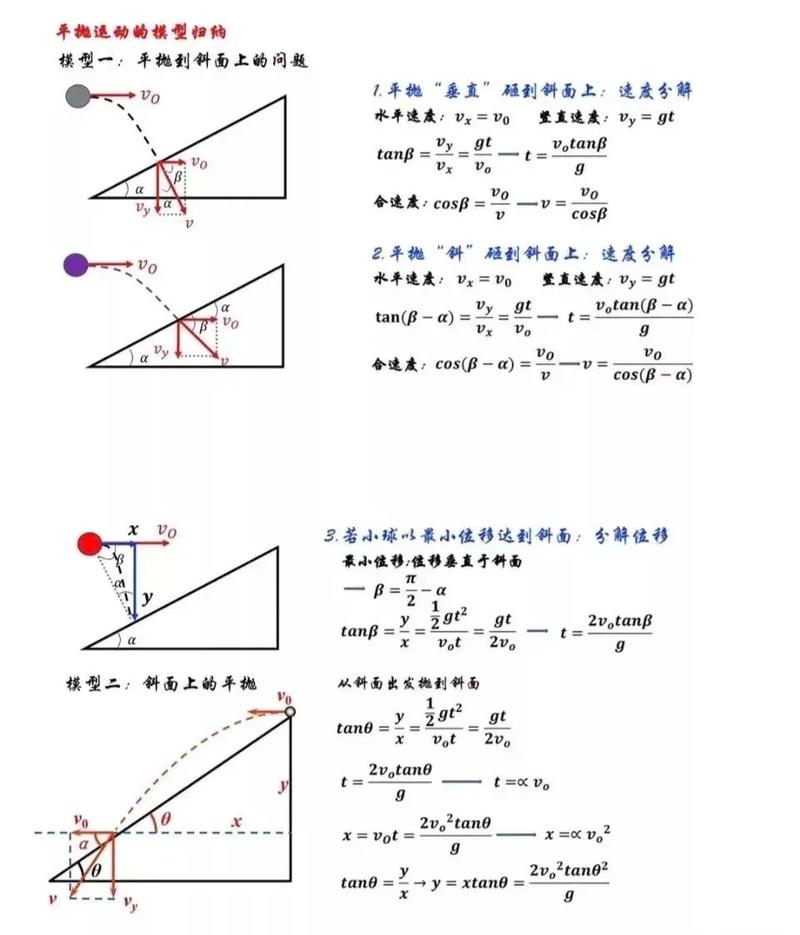
运动的独立性原理
平抛运动可以看作是两个简单、独立的直线运动的合运动:
- 水平方向:不受力(或忽略空气阻力),做匀速直线运动。
- 竖直方向:只受重力,做自由落体运动(初速度为零的匀加速直线运动)。
关键点:这两个分运动是同时进行、互不干扰的,它们的时间是相同的,这是我们联系两个方向运动的最重要桥梁。
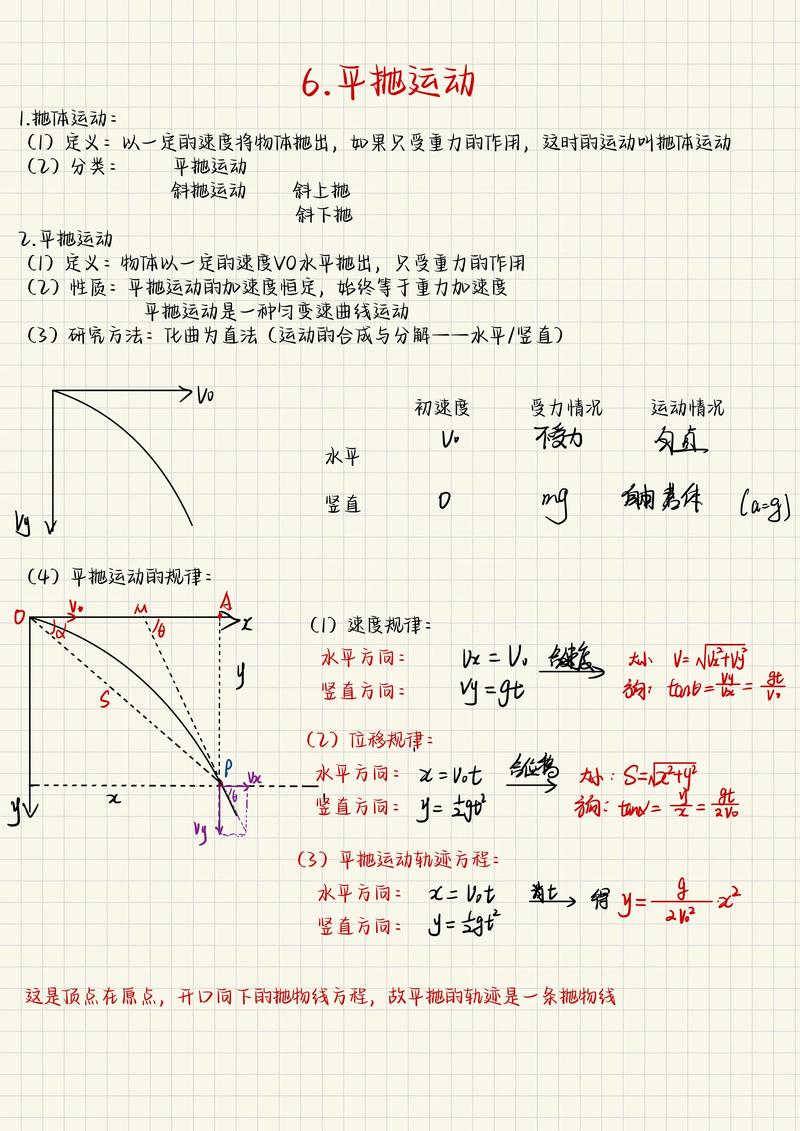
基本分解与核心公式
基于上述思想,我们可以将平抛运动分解到水平和竖直两个坐标轴上。
| 运动性质 | 水平方向 (x轴) | 竖直方向 (y轴) |
|---|---|---|
| 受力情况 | 合外力为 0 | 合外力为重力 mg |
| 运动性质 | 匀速直线运动 | 匀加速直线运动 (自由落体) |
| 初速度 | v₀x = v₀ (初速度) |
v₀y = 0 |
| 加速度 | ax = 0 |
ay = g (重力加速度) |
| 任意时刻速度 | vx = v₀ (保持不变) |
vy = gt |
| 任意时刻位移 | x = v₀t |
y = ½gt² |
| 合速度 | v = √(vx² + vy²) = √(v₀² + (gt)²) 方向: tanθ = vy / vx = gt / v₀ (θ为速度与水平方向夹角) |
核心技巧:只要题目中涉及到时间,你就可以在 x = v₀t 和 y = ½gt² 之间进行转换,我们可以从竖直方向的位移公式中解出时间 t,再代入水平方向的公式中。
常见问题类型的解题技巧
技巧1:求飞行时间(“时间”是桥梁)
飞行时间由高度决定,与初速度 v₀ 无关。
- 模型:物体从高度
h处平抛。 - 分析:飞行时间
t就是物体做自由落体运动下落高度h所用的时间。 - 公式:
h = ½gt²=>t = √(2h/g) - 应用:求出时间
t后,就可以计算水平射程x = v₀t = v₀√(2h/g)。
口诀:时间看高度,射程看速度和高度。
(图片来源网络,侵删)
技巧2:求速度(分解合速度)
中给出的速度往往是合速度,需要分解到水平和竖直方向。
- 模型:已知某时刻物体的合速度
v和其与水平方向的夹角 。 - 分析:
- 水平分速度
vx = v * cosθ,由于水平方向是匀速运动,这个分速度就等于初速度v₀。 - 竖直分速度
vy = v * sinθ。
- 水平分速度
- 公式:
- 求初速度:
v₀ = vx = v * cosθ - 求该时刻所用时间:由
vy = gt得t = vy / g = (v * sinθ) / g - 求下落高度:
y = ½gt² = ½g * [(v * sinθ) / g]² = (v²sin²θ) / (2g)
- 求初速度:
口诀:已知合速度,分解成两半;水平定初速,竖直求时间。
技巧3:斜面上的平抛运动(建立坐标系)
这是最常见的难点,关键在于如何建立坐标系。
- 模型:物体从斜面顶端平抛,落在斜面上。
- 技巧:不要总是建立水平竖直的坐标系! 为了利用“末速度方向与斜面平行”或“末位移方向沿斜面”这一条件,应该沿斜面和垂直于斜面建立坐标系。
- 分析:
- 将重力加速度
g分解到两个新坐标轴上:- 沿斜面向下:
g_∥ = g * sinα - 垂直斜面向下:
g_⊥ = g * cosα
- 沿斜面向下:
- 平抛运动在两个新方向上的分运动仍然是匀变速直线运动。
- 关键条件:物体落在斜面上时,其位移方向与斜面平行,这意味着在垂直于斜面方向上的位移
y_⊥ = 0。
- 将重力加速度
- 公式:
- 沿斜面方向:
x_∥ = v₀ * cosα * t + ½ * g * sinα * t² - 垂直斜面方向:
y_⊥ = v₀ * sinα * t - ½ * g * cosα * t² - 利用条件
y_⊥ = 0,可以解出飞行时间t。 v₀ * sinα * t - ½ * g * cosα * t² = 0t * (v₀ * sinα - ½ * g * cosα * t) = 0- 解得
t = 0(抛出时刻) 或 *`t = (2v₀ sinα) / (g cosα) = (2v₀ / g) tanα`**
- 沿斜面方向:
- 应用:求出时间
t后,可以代入x_∥求出沿斜面的位移,或代入速度分解公式求末速度。
口诀:遇到斜面抛,坐标斜着找;垂直方向位移零,时间就好求。
(图片来源网络,侵删)
技巧4:类平抛运动(推广思想)
当物体受到一个恒定的、与初速度方向垂直的力时,其运动规律与平抛运动完全类似,只需将 g 替换为相应的加速度 a 即可。
- 模型:带电粒子在正交的匀强电场和磁场中运动(仅电场力或仅洛伦兹力),或其他类似场景。
- 分析:
- 沿初速度方向:匀速直线运动。
- 沿力的方向:初速度为零的匀加速直线运动。
- 公式:将平抛公式中的
g替换为a = F/m。x = v₀ty = ½at²vy = at
解题步骤总结
- 画图:画出运动轨迹示意图,标出已知量和未知量。
- 建系:根据题目特点,选择合适的坐标系(通常是水平竖直,斜面问题用斜坐标系)。
- 分解:将初速度和加速度分解到两个坐标轴上。
- 找桥梁:寻找两个分运动的联系,时间
t通常是唯一的桥梁。 - 列方程:根据运动学公式,在两个方向上分别列出方程。
- 求解:联立方程,解出未知量。
经典例题(斜面模型)
从倾角为 α 的斜面顶端,以初速度 v₀ 水平抛出一小球,小球再次落到斜面上时,求飞行时间 t 和小球在空中运动时的速度大小。
解析:
- 画图建系:如上文所述,沿斜面和垂直斜面建立坐标系。
- 分解加速度:
g_∥ = g * sinα(沿斜面向下)g_⊥ = g * cosα(垂直斜面向下)
- 分解初速度:
v_∥ = v₀ * cosα(沿斜面向下)v_⊥ = v₀ * sinα(垂直斜面向上)
- 列方程:
- 垂直斜面方向:
y_⊥ = v_⊥ * t - ½ * g_⊥ * t² - 落在斜面上时,
y_⊥ = 0。 v₀ * sinα * t - ½ * g * cosα * t² = 0
- 垂直斜面方向:
- 求解时间:
t * (v₀ * sinα - ½ * g * cosα * t) = 0- 解得
t = 0(舍去) 或 *`t = (2v₀ sinα) / (g cosα) = (2v₀ / g) tanα`**。
- 求解速度:
- 沿斜面方向速度:
v_∥' = v_∥ + g_∥ * t = v₀cosα + gsinα * (2v₀tanα/g) = v₀cosα + 2v₀sin²α/cosα = v₀(cos²α + 2sin²α)/cosα - 垂直斜面方向速度:
v_⊥' = v_⊥ - g_⊥ * t = v₀sinα - gcosα * (2v₀tanα/g) = v₀sinα - 2v₀sinα = -v₀sinα(负号表示方向向下) - 合速度大小:
v = √(v_∥'² + v_⊥'²)(代入上式化简即可)
- 沿斜面方向速度:
通过以上系统性的分解和技巧应用,平抛运动问题就变得有章可循了,核心就是分而治之,以时间桥接。